Percentage Types 21 – 30
Expenditure = Price * Consumption
In question Expenditure is same; price or Consumption increases or decreases to find consumption or price increases or decrease use these formula
increase “+” value or Decrease “-” value

In question, expense price and Consumption are given for increase or decrease to find Expenditure increase or decrease using successive % formula
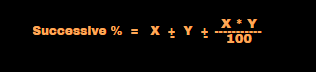
In question Price and Expenditure is given for increase or decrease to find Consumption increase or decrease using the below formula
Initial value = 100%

In question Consumption and Expenditure is given for increase or decrease to find Price increase or decrease using the below formula
Initial value = 100%

Decrease or increase % of consumption or price = Final value % – 100%
Type: 21
The price of petrol has been increased by 10% in the new budget. The passenger of a motor vehicle can reduce the consumption to how many % so that his total expenditure on petrol remains the same?
Solution :
Expenditure = Price * Consumption
In these questions, expenditure is the same; price increases or decreases to find consumption increased or decrease Use these formula
increase “+” value or Decrease “-” value

Type: 21.1
When the price of rice is increased by 25 percent, a family reduces its consumption such that the expenditure is only 10 percent more than before. If 40 kg of rice is consumed by the family before, then find the new consumption of the family.
Solution :
In these questions, Price and Expenditure are given for increase or decrease to find Consumption increase or decrease using the below formula

Type: 22
Due to a 25% reduction in the price of wheat per kg, John can buy 5 kg more for ₹600. What is the original price of wheat per kg?
Solution :
Reduction price % → more KGS
Original price % = 100% – Reduction%
New price % = 100%
Original price % = 100% – 25% = 75%
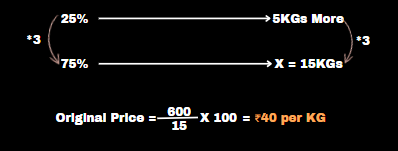
Type: 23
Mridula operates a small shop of pets. Her expenditure details are as follows: 90% on procurement and 10% on rent and electricity. If she monthly spends ₹15,000 on rent and electricity, then how much does she spend monthly on procurement?
Solution :
10% rent → 15000
90% procurement → X
X = ₹135000
Type: 24
An investor invests 1/2 part of his money at 5%, 1/4 part at 10%, and the rest at 8%. After 2 years, his income is ₹2800 then, find the total amount
Solution :
Assume Total Parts = 4
1/2 Part = 1/2 * 4 = 2 parts = 2 * 5% = 10%
1/4 Part = 1/4 * 4 = 1 parts = 1 * 10% = 10%
Remaining parts = 1 part = 1*8% = 8%
Total Amount = 4 Parts * 100% = 400%
Total interest = 10%+10%+8% = 28%per 1 years
Total interest = 2800/2 = ₹1400
28% → ₹1400
400% → X
X = ₹20000
Type: 25
In a solution, the quantity of common salt in 320 gm of water is 33 gm. Calculate the concentration % of the solution in the context of mass by mass percentage.
Solution :

the concentration % of the solution = 9.35%
Type: 26
A’s salary is 20% less than B’s salary. What percentage of B’s salary is more than A’s salary?
Solution :
This type of question is X is % more than Y, find Y is how much % less than X
or
This type of question is X is % less than Y, find Y is how much % More than X
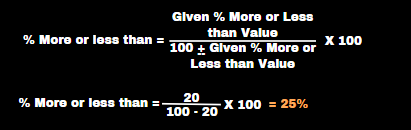
Type: 27
By what percent does the curved surface area of a cylinder decrease if the radius is increased by 10% and the height is decreased by 40%?
Solution :
In this type of question, use this formula for areas in mensuration, i.e, if any two % values are multiplied, use two successive % formulas, and if any three % values are multiplied, use three successive % formulas

% Decrease area = – 34%
-ve indicates the decreased value
Type: 28 (election-based questions)
In an election, 90% of those entitled to vote cast their ballot; 80% of the votes cast were valid. The winner got 60% of the valid votes. If the winner got 64800 votes, what was the number of people entitled to vote?
Solution :
Note: You must carefully read these election-based questions

Total Votes x 90% * 80% * 60% = 64800
Total Votes = 150000
Type: 28.1
In an election, a candidate with 37% of the votes loses by a difference of 520000 votes to the winning candidate. What is the total number of votes cast in that election with two contestants?
Solution :
Note: You must carefully read these election-based questions
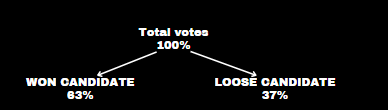
Winning Margin = Won % – Loose %
63% – 37% = 26% → 520000
100% → X
X = 2000000
In an election, a candidate got 62% of the total votes and won the election by 35640 votes. What is the total number of votes cast if no vote is declared invalid?
Solution :
Note: You must carefully read these election-based questions
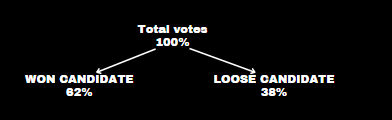
Winning Margin = Won % – Loose %
62% – 38% = 24% → 35640
100% → X
X = 148500
Type: 28.2
In an election, there were only two candidates. The winning candidate got 48% of the total votes. His opponent got 6800 votes,, which was 34% of the total votes. Some of the votes were invalid. The winning margin of the candidate who won the election and the number of invalid votes respectively, are:
Solution :
Note: You must carefully read these election-based questions
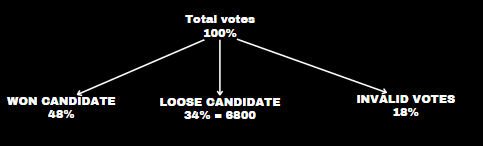
Winning Margin = Won % – Loose %
Winning Margin = 48% – 34% = 14%
34% → 6800
Invalid votes = 18% → X = 3600
Winning Margin = 14% → Y = 2800
Type: 28.3
In an election between two candidates, 75% of the voters enrolled in the election cast their votes, out of which 2% were declared invalid. A candidate got 9261 votes, which were 75% of the valid votes. The total number of voters enrolled in that election were
Solution :
Note: You must carefully read these election-based questions
In this questions use this way easily
Total Votes * cast/valid% = Candidate got votings
X * 75% * (100% – 2%) * 75% = 9261 VOTES
X = 16800
Type: 28.4
In an election, there were only two candidates. The losing candidate got 48% of the total votes. His opponent got 6000 more votes and won by a margin of 3% of the votes. What was the number of invalid votes?
Solution :
Note: You must carefully read these election-based questions

Actual winning margin = 52% – 48% = 4%
But in question margin % is given 3%so remaining 1% is invalid vote%
3% → 6000
1% → X
invalid votes = 2000
Type: 28.5
In an election between two candidates, 30% of the electorate did not cast their votes. 20% of the votes polled were found invalid. The winning candidate got 64% of the valid votes and won by a majority of 3136 votes. Find the number of voters enrolled in the voter list.
Solution :
Note: You must carefully read these election-based questions

Winning Margin = Won% – Lose% = 64% – 36% = 28%
Total Votes * cast/valid% * Winning Margin% = Winning Margin Votes
X * (100% – 30%) * (100% – 20%) * 28% = 3136 Votes
Total Votes = 20000 Votes
Type: 28.6
If the curved surface area of a cylinder is increased by 20% and the height is decreased by 4%, then the net decrease or increase in the volume will be:
Solution :
Note: You must carefully read these election-based questions
You can use this way to increase or decrease volume
Curved surface area of cylinder = 2πrh
Ignore 2π value
r.h. = 20% increase
r * (100%-4%) = (100%+20%)
r = 1.25 * 100 = 125%, i.e (100% + 25%)
r = 25% increase
or you can solve this using two-values successive % formula
Volume of cylinder = πr²h
Ignore numerical and π values
r²h = 25% * 25% * -4%
using three values successive % formula to solve the above values is 25%, 25%,-4%
Volume increase = 50% increase
Type: 28.7
A total of 750,000 voters participated in the election. A candidate received 3,825,000 votes, which was 60% of the total valid votes. What was the percentage of invalid votes in the election?
Solution :
Note : You must carefully read these election-based questions
Total Valid Votes = 750000
60% Valid votes → 382500
100% Valid votes → X
X = 637500
invalid votes = 750000 – 637500 = 112500
invalid votes % = 112500/750000 = 15%
Type: 28.8
In an election between two candidates, 20% of the voters on the voters list did not cast their votes, and 80 voters cast their ballot papers blank. The winner secured 45% of all the voters in the list, and he got 280 votes more than his rival. The number of voters on the list was:
Solution :
Note : You must carefully read these election-based questions
Total Valid Votes = 100X
Valid Votes = 100x – 20X = 80X – 80
80 is votes exclude
Winning % = 45% = 45X
Losser % = Valid Votes – Winner %
= (80X – 80) – 45X
= 35X – 80
Winning Margin = Won % – Loose %
Winning Margin = 280 = 45X – (35X – 80 )
100X = 2000
Type: 29
A contractor reduces the working time of a week (Monday to Saturday) from 48 hours to 36 hours for his workers without changing the payment. What is the percentage increase in the hourly rate?
Solution :

Type: 30
Suresh could save 20% of his income. But 4 years later, when his income increased by 40%, he could save only the same amount as before. By what percentage did his expenditure increase?
Solution :
Income = Expenditure + Saving

For more updates on Percentage Types 21 – 30 and other aptitude tricks, stay tuned to Exam Guru!



Leave a Comment