Percentage Types 1 – 20
Type: 1
What percentage is 15 minutes of 1 1/2 days?
Solution :
If any question for percentages numerator value units and denominator value units are same
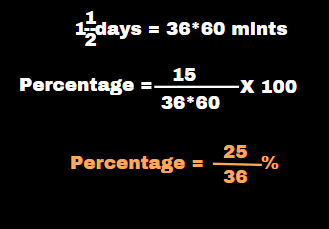
Type 1.1
What is the percentage form of the ratio 1:8?
Solution :
numerator value: denominator value
1: 8
Percentage = 1/8 * 100
Percentage = 12.5%
Type: 1.2
Find the number, which is 30% more than 240.
Solution :
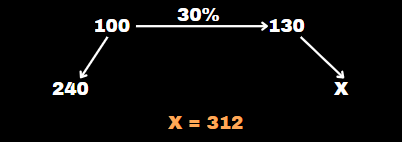
Type: 1.3
If 27.5% of a number is 11, then the number is:
Solution :
K X 27.5% = 11
K = 40
Type: 1.4
If 75% of a number is added to 75, then the result is the number itself. The number is:
Solution :
75% a number + 75 = a number itself
assume a number = K
75% * K + 75 = K
K = 300
Type: 1.5
The difference between 48% and 38% of a number is 354. What is 58% of that number?
Solution :
48% – 38% = 354
10% → 354
58% → K
K = 2053.2
Type: 1.6
Which number is 40% less than 80?
Solution :
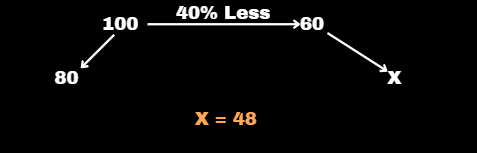
Type: 1.7
If 40% of 70 is x % more than 30% of 80, then find the value of ‘x’.
Solution :
If you can find more than or less than % value, you can use this way
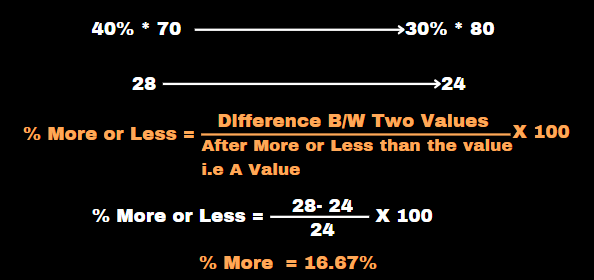
Type: 1.8
Two numbers, A and B, are less than a third number, C, by 15% and 32%, respectively. By what percentage is number B less than number A?
Solution :

Type: 1.9
40% of a number is 46 less than 4/5 of that number; find the number.
Solution :
40% * Number = (4/5 * Number) – 48
Assume a Number = K
40% * K= (4/5 * K) – 48
K = 115
Type: 1.10
25% of a number is 7 more than 30% of another number. The difference between the numbers is 29. What are the numbers?
(a) 39 and 10 (b) 40 and 11 (c) 34 and 5 (d) 37 and 8
Solution :
25% * K = 30% * P + 7
Assume one number = K
Another number = P
K – P = 29
Don’t calculate total values; simply put the given values from the options you get to quickly solve the question
K = 34, P = 5
Type: 2
If 20% of a = b, then b% of 20 is equals to which of the following?
(a) 20% of a (b) 4% of a (c) 5% of a (d) 30% of a
Solution :
20% of a = b
b% of 20 = a/5 % * 20
b% of 20 = 4% of a
Type: 1.11
In an examination Sunita scored 90% of what Anita scored, while Anita’s score was 110% of want Vinita scored if Sunita scored 198 marks in the examination, how many marks did Vinita score ?
Solution :
These questions are interlinked questions
Sunitha = 90% * Anitha; Anita = 110% * Vinitha
Sunitha = 198 Marks
Put the Sunitha mask above you get vinita marks
vinita = 200
Type : 3
The population of the village increased from 18000 to 22500. What is the increased percentage?
Solution :

Type: 4
The population of a town increased by 10% and 20% in two successive years but decreased by 25% in the third year. Find the ratio of the population in the third year to that of 3 years ago.
Solution :
In this type of question, you can solve the ratio & proportion method easily for you
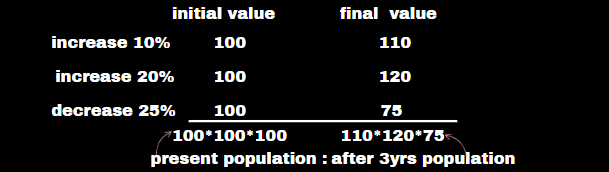
Note: You must read the question to what is he ask
in question ask after 3 years population: present population
110*120*75 : 100*100*100 = 99 : 100
Type: 5
The current population of the town is 15,625. It increases by 8% and 12% in two successive years but decreases by 22% in the third year. What is the population of the town at the end of the third year?
Solution :
This type two type you can solve

Don’t calculate total value you L.H.S multiples = RHS multiples; i.e., in LHS 7 Multiple is there, 7*16 = 112 so Answer also 7 multiples
Type: 6
20% of the population of a city died due to war, and of the remaining population, 5% died in an epidemic. If the present population of the city is 15,200, then find the population of the city before the war.
Solution :
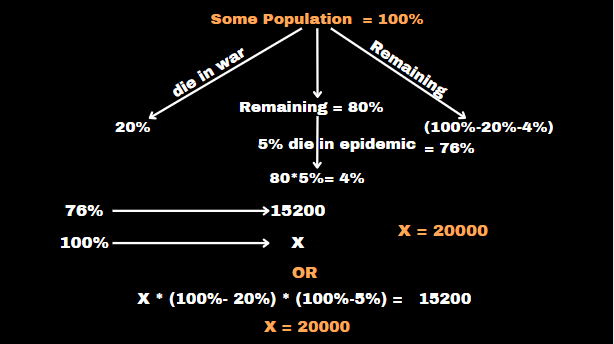
Type: 7
The population of a town increases at the rate of 10% every year. The present population is 1,000. In how many years will the population become 1,331?
Solution :

Type: 8
A bacterial population increases at the rate of 6% in the first 10 minutes and then 10% in the next 10 minutes. What is the overall percentage increase in the population at the end of 20 minutes?
Solution :
this type questions some X% at t1 time and Y% at t2 time find the overall percentage at t1+t2 time

Type: 9
The population of a town is 10,000. If the male population increases by 5% and the female population by 10%, the population will become 10,800. How much of the town’s present population is female?
Solution :
Using alligation and mixture method, two type
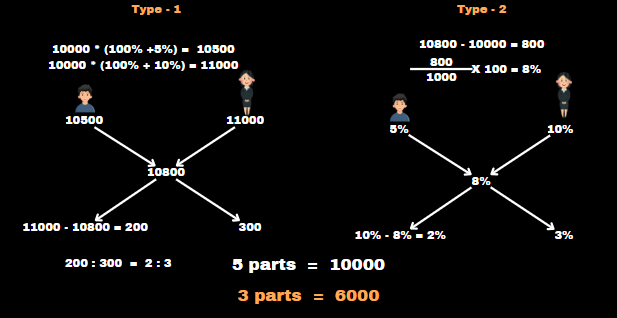
Type: 10
If Anju scored 68 out of 80 in Hindi, 46 out of 60 in Mathematics, 74 out of 90 in Science, and 35 out of 45 in English, then in which subject did Anju score the maximum percentage of marks?
Solution :
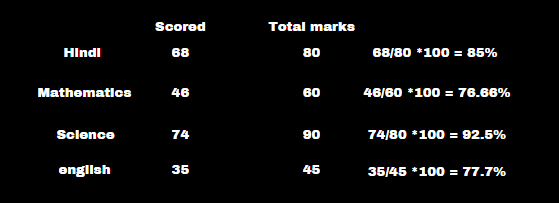
Max Percentage = 92.5% = Science
Type: 11
Two students appeared for an entrance examination. One of them secured 15 marks more than the other and his marks are 80% of the sum of their marks. What are the marks obtained by each of them?
Solution :
One student = X Other student = Y
X = 15 + Y X = 80% (X+Y)
80x = 15 + 20x; x/(x+y) = 80/100
60x = 15
20x = 5 = Y
X = 5 + 15 = 20
Type: 12
Tony should get 40% of the total marks to pass. He obtained 120 marks and failed by 30 marks. What are the total marks?
Solution :
Pass Marks = Obtained Marks + Failed Marks
Pass Marks = 120 + 30 = 150 Marks
40% Total Marks = 150
Total Marks = 375 Marks
Type: 12.1
Vimal secured 46% marks in the exam and failed to qualify in the exam by 10 marks. If he secured 52% marks, he would have secured 8 marks more than what was the minimum qualifying marks. What were the minimum marks one had to score to qualify for the exam?
Solution :
This type of question uses the below way
Failed marks% & More marks % difference→Failed marks & More marks sum
52% – 46% → 10 Marks + 8 Marks
100% = Total Marks → 300
Minimum Marks or Pass Marks = 46% * Total Marks + 10 or 56% * Total Marks – 8
Minimum Marks or Pass Marks = 148
Max marks = Total Marks = 300
Type: 13
The average mark obtained in mathematics by the students of the class was 70. The average marks obtained by the boys is 20% more than the average marks obtained by the girls. If the ratio of the number of boys to that of girls is 3 : 2, then the average marks obtained by the girls is
(a) 65 (b) 62.5 (c) 63 (d) 63.5
Solution :
This type of question doesn’t calculate the total value; you can put the value or given options
average of boys is 20% more than average marks girls
avg boys : avg girls = 100 : 120 = 5 : 6

You can put average girl value in 6x = 62.5
If you put the value of 62.5, you can the ratio = 3.2
So, all questions are not calculated. Some questions are to put the value for given options you get the answer
Type: 14
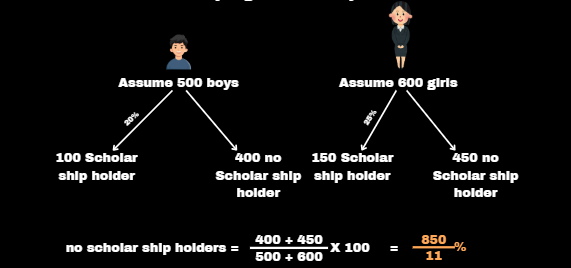
In the school, the ratio of the number of boys to girls is 5:6. 20% of the boys and 25% of the girls are scholarship holders. How many students did not get a scholarship?
Solution :
Assume boys : girls = 5 : 6 only
Type: 15
In an examination, 80% of students passed in physics and 70% of students passed in chemistry, while 15% of students failed in both subjects. If 325 students passed in both the subjects, find the total number of students who appeared in the examination.
Solution :
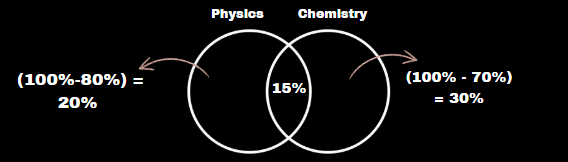
Remember middle value is failed, so physics and chemistry values also you give failed students
Pass % = sum of failed students % in the above diagram
Pass % = 20%+15%+30% = 65%→325
100%→X = 500
Type: 16
If Mohan secured 72% marks in physics and 68% in chemistry, what percentage of marks did Mohan get in both subjects together, assuming that the two subjects have equal weightage?
Solution :
total marks of the both subjects are equal you can solve this two types

Type: 16.1
In order to qualify in an examination, one has to secure 50% of the overall marks. In the examination consisting of two papers, a student secured 40% in the first paper of 200 marks. Minimum, what percentage of marks should be secured in the second paper of 150 marks to qualify in the examination?
Solution :
using alligation & mixture method

Type: 17
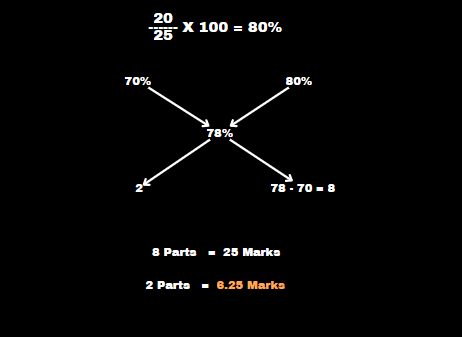
Durba got 70% marks in an exam. He obtained 20 out of 25 marks in another exam. If his total score is 78% then what were the maximum marks of the first exam?
Solution :
Type: 17.1
Rahul had to appear for a test in four subjects. In the first three subjects the maximum marks were 50 each, in which Rahul secured 60% on an average. In the fourth subject Rahul scored 54 marks and his overall percentage is 64%. What were the maximum marks in the fourth subject ?
Solution :
Total marks of 3 subject = 50 + 50 + 50 = 150
He gained = 150* 60% = 90
He gained marks Total marks
first 3 subjects 90 150
fourth subject 54 Y
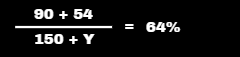
Y = 75
Type : 18
A student had got few marks from maximum marks probably. These marks were 75% as %. If one more question would be added of one mark in the exam then his obtained marks percentage would have 76%. What were the initial maximum marks of the exam?
Solution :
Some marks = X
X→75%
After 1 more question added
X + 1 → 75%
% Difference → no.of marks more or less (100% – after marks adding percentage)
(76% – 75%)*X→1 Marks (100% – 76%)
X% →24% Marks
X = 24 Marks
Type 19 (income-based problems)
Tanvi saves ₹5,000 from her salary every month after spending 80% of her monthly salary. Tanvi’s salary is :
Solution :
Income = Expenditure + Saving
100% = 80% + 20%
20% →5000
100% →X
X = 25000
Type: 19.1
The income of Raman is ₹45,000. He saves 12.5% of his income. If his income increases by 18% and expenditure increases by 20%, then his savings will :
Solution :
Income = Expenditure + Saving
100% = 87.5% + 12.5%

X = 5850
Saving is increase = 5850 – 5625 = 225
Type: 19.2
On average Pramod uses 10% of his monthly income to fill petrol in his car. The rest 80% is spent on home expenditure and he saves 10% of his salary. On a monthly basis, if he spends ` 24,000 on household expenditure, then what is his annual income?
Solution :
Income = Expenditure + Saving
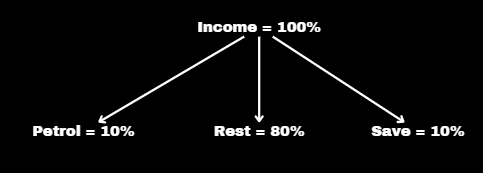
80% →24000
100% →30000
Type: 19.3
Moris spent 25% of his income on food. He got an increment of ₹1000, but he did not increase his expenditure on foodstuffs. Therefore, his expense of food expenses decreased to 20%. What was his initial income?
Solution :
Income = Expenditure + Saving
Income is increasing Expenditure is the same use this way
In question saving is not given, so it’s zero
Difference of %values → increment value * food decreased to 20%
25% – 20%→1000*20%
100% →X
X = 4000
Type: 19.4
Vikas spends 80% of his salary. His salary is increased by 25% and his expenditure increased by 15% What is the percentage increase in his savings?
Solution :
Income = Expenditure + Saving
100% = 80% + 20%
increase use “+” value and decrease use “-” value

Type: 19.5
The sum of the salaries of A and B together is ₹4300. A spends 95% of his salary and B, 80% of his salary. If their savings are the same, what is A’s salary ?
Solution :
Income = Expenditure + Saving
Saving is same
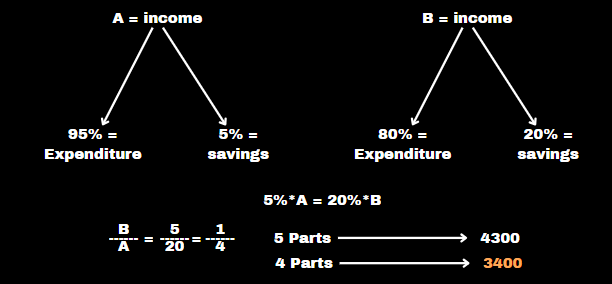
Type: 19.6
The annual income of Somnath is ₹24,00,000. He pays ₹40,000 EMI for his vehicle every month. What percentage of his monthly income is spent on EMI?
Solution :
Income = Expenditure + Saving
You should must read question
in question ask % value of monthly but in he is given yearly income
monthly income = 2400000/12 = 200000

Montly EMI % = 20%
Type: 19.7
From the salary of Hari, 15% is deducted as house rent, 20% of the remaining amount is spent on children’s education and 10% of the remaining balance is his medical expenses. Finally, he is left with ₹42,840. Find his total salary.
Solution :
Income = Expenditure + Saving
income * (100%-P1%) * (100%-P2%) = reamining balance
X * (100%-15%) * (100%-20%) * (100%-10%) = 42840
In this type of question, you can easily identify for spending remaining balances uses this way
X = 70000
Type: 19.8
Arun’s income is 150% of Bala’s income. Chandu’s income is 120% of Arun’s income. If the total income of Arun, Bala, and Chandu is ₹86000, then find Chandu’s income.
Solution :
using ratio & proportion method
Assume Bala income = 100
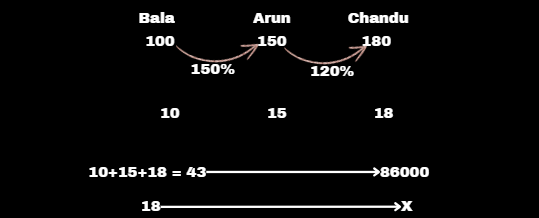
X = 36000
Don’t calculate the total value because 18 is a multiple of 9, so answer is multiple of 9
Type: 20 (Successive % Questions)
The price of a bike was increased by 10% and then again increased by 8%. The net percentage increase in the price of the bike is:
Solution :
Successive % of two values
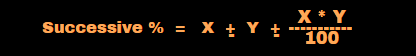
increase “+” value or Decrease “-” value
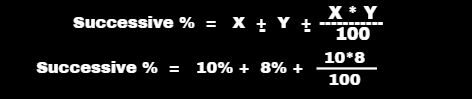
Successive % = 18.8
Type: 20.1
The profit of a company increased by 10% from April to May, then it decreased by 20% from May to June and again increased by 50% from June to July. What was the % growth in profit from April to July?
Solution :
Successive % of three values
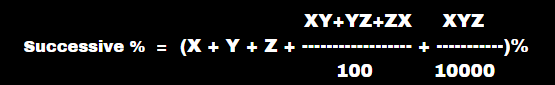
or let give x%,y%.z% first x% and y% using successive % formula to get one answer after remaining z% using same successive % for these two value you get answer
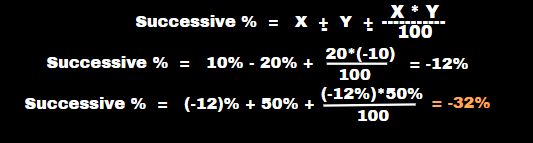
For more updates on Percentage Types 1 – 20 and other aptitude tricks, stay tuned to Exam Guru!



Leave a Comment